Математические действия с дробями. Сложные выражения с дробями. Порядок действий
В данной статье репетитором по математике и физике рассказано о том, как производить элементарные операции с обыкновенными дробями: сложение и вычитание, умножение и деление. Рассказано о том, как представить смешанное число в виде неправильной дроби и наоборот, а также о том, как сокращать дроби.
Сложение и вычитание обыкновенных дробей
Напомним, что знаменателем дроби называется число, которое находится снизу , а числителем — число, которое находится сверху от дробной черты. Например, у дроби число является числителем, а число — знаменателем.
Общим знаменателем является наименьшее возможное число, которое делится и на знаменатель первой дроби, и на знаменатель второй дроби.
Пример 1 . Сложить две дроби: .
Воспользуемся описанным выше алгоритмом:
1) Наименьшее число, которое делится и на знаменатель первой дроби, и на знаменатель второй дроби, равно . Это число и будет являться общим знаменателем. Теперь нужно привести обе дроби к общему знаменателю.
2) Складываем полученные дроби: ![]() .
.
Умножение обыкновенных дробей
Иными словами, для всех действительных чисел , , , , справедливо равенство:
![]()
Пример 2 . Перемножить дроби: .
Для решения данной задачи воспользуемся представленной выше формулой: ![]() .
.
Деление обыкновенных дробей
Иными словами для всех действительных чисел , , , , , справедливо равенство:

Пример 3 . Разделите дроби: .
Для решения этой задачи воспользуемся приведенной выше формулой: ![]() .
.
Представление смешанного числа в виде неправильной дроби
Разберемся теперь, как быть, если требуется выполнить какую-либо операцию с дробями, представленными в виде смешанных чисел. В этом случае сперва нужно представить смешанные числа в виде неправильных дробей, а затем выполнить необходимую операцию.
Напомним, что неправильной называется дробь, у которой числитель больше или равен знаменателю.
Напомним также, что у смешанного числа есть дробная часть и целая часть . Например, у смешанного числа дробная часть равна , а целая часть равна .
Пример 4 . Представить смешанное число в виде неправильной дроби.
Воспользуемся представленным выше алгоритмом: ![]() .
.
Пример 5 . Представьте неправильную дробь в виде смешанного числа.
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно "не очень..."
И для тех, кто "очень даже...")
Итак, что из себя представляют дроби, виды дробей, преобразования - мы вспомнили. Займёмся главным вопросом.
Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями - это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:

Короче, в общем виде:

А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:

Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:

Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:

И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений...
Дорешайте уж пример самостоятельно. Не логарифм какой... Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах... И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да...
Итак, нам надо сложить два дробных выражения:
![]()
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:

И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби - на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки...
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:

Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе - само число, в знаменателе - единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами - то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению - вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой - повторили. Можно и провериться. Порешаем немного?)
Вычислить:

Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей - в следующем уроке. Там же и задания на все действия с дробями.
Если Вам нравится этот сайт...
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся - с интересом!)
можно познакомиться с функциями и производными.
Условимся считать, что под "действиями с дробями" на нашем уроке будут пониматься действия с обыкновенными дробями. Обыкновенная дробь - это дробь, обладающая такими атрибутами, как числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой, отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби особых затруднений не вызывают. Итак, вперёд!
Две дроби и называются равными, если .
Например, , так как
Равными также являются дроби и (так как ), и (так как ).
Очевидно, равными являются и дроби и . Это означает, что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной: .
Это свойство называется основным свойством дроби.
Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателя дроби. Если числитель и знаменатель дроби умножить на -1, то получим . Это означает, что значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
Сокращение дробей
Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью, равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.
Пусть, например, дана дробь . Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
![]() .
.
В общем случае сокращение дроби возможно всегда, если числитель и знаменатель не являются взаимно простыми числами. Если числитель и знаменатель - взаимно простые числа, то дробь называется несократимой.
Итак, сократить дробь - это значит разделить числитель и знаменатель дроби на общий множитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.
Пример 1. Сократить дробь
Решение. Для разложения числителя на множители, представив предварительно одночлен - 5xy в виде суммы - 2xy - 3xy , получим

Для разложения знаменателя на множители используем формулу разности квадратов:
В результате
![]() .
.
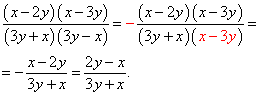
Приведение дробей к общему знаменателю
Пусть даны две дроби и . Они имеют разные знаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им, причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменатель дроби на 7, получим
Умножив числитель и знаменатель дроби на 5, получим
Итак, дроби приведены к общему знаменателю:
![]() .
.
Но это не единственное решение поставленной задачи: например, данные дроби можно привести также к общему знаменателю 70:
![]() ,
,
![]()
и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.
Рассмотрим ещё один пример: приведём к общему знаменателю дроби и . Рассуждая, как в предыдущем примере, получим
![]() ,
,
![]() .
.
Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведение знаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120 .
Так как 120:4=5, то чтобы записать дробь
со знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительным
множителем. Значит ![]() .
.
Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби
на дополнительный
множитель 4, получим ![]() .
.
Итак, данные дроби приведены к общему знаменателю.
Наименьшее общее кратное знаменателей этих дробей является наименьшим возможным общим знаменателем.
Для дробных выражений, в которые входят переменные, общим знаменателем является многочлен, который делится на знаменатель каждой дроби.
Пример 2. Найти общий знаменатель дробей и .
Решение. Общим знаменателем данных дробей является многочлен
,
так как он делится и на ,
и на .
Однако этот многочлен не единственный, который может быть общим знаменателем данных дробей.
Им может быть также многочлен ![]() ,
и многочлен
,
и многочлен ![]() , и
многочлен
, и
многочлен ![]() и т.д.
Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без
остатка. Такой знаменатель называется наименьшим общим знаменателем.
и т.д.
Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без
остатка. Такой знаменатель называется наименьшим общим знаменателем.
В нашем примере наименьший общий знаменатель равен . Получили:
![]() ;
;
![]() .
.
Нам удалось привести дроби к наименьшему общему знаменателю. Это произошло путём умножения числителя и знаменателя первой дроби на , а числителя и знаменателя второй дроби - на . Многочлены и называются дополнительными множителями, соответственно для первой и для второй дроби.
Сложение и вычитание дробей
Сложение дробей определяется следующим образом:
![]() .
.
Например,
![]() .
.
Если b = d , то
![]() .
.
Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложить числители, а знаменатель оставить прежним. Например,
![]() .
.
Если же складываются дроби с разными знаменателями, то обычно приводят дроби к наименьшему общему знаменателю, а потом складывают числители. Например,
![]() .
.
Теперь рассмотрим пример сложения дробных выражений с переменными.
Пример 3. Преобразовать в одну дробь выражение
![]() .
.
Решение. Найдём наименьший общий знаменатель. Для этого сначала разложим знаменатели на множители.
Эта статья про обыкновенные дроби . Здесь мы познакомимся с понятием доли целого, которое приведет нас к определению обыкновенной дроби. Дальше остановимся на принятых обозначениях для обыкновенных дробей и приведем примеры дробей, скажем про числитель и знаменатель дроби. После этого дадим определения правильных и неправильных, положительных и отрицательных дробей, а также рассмотрим положение дробных чисел на координатном луче. В заключение перечислим основные действия с дробями.
Навигация по странице.
Доли целого
Сначала введем понятие доли .
Предположим, что у нас есть некоторый предмет, составленный из нескольких абсолютно одинаковых (то есть, равных) частей. Для наглядности можно представить, например, яблоко, разрезанное на несколько равных частей, или апельсин, состоящий из нескольких равных долек. Каждую из этих равных частей, составляющих целый предмет, называют долей целого или просто долей .
Заметим, что доли бывают разные. Поясним это. Пусть у нас есть два яблока. Разрежем первое яблоко на две равные части, а второе – на 6 равных частей. Понятно, что доля первого яблока будет отличаться от доли второго яблока.
В зависимости от количества долей, составляющих целый предмет, эти доли имеют свои названия. Разберем названия долей . Если предмет составляют две доли, любая из них называется одна вторая доля целого предмета; если предмет составляют три доли, то любая из них называется одна третья доля, и так далее.
Одна вторая доля имеет специальное название – половина . Одна третья доля называется третью , а одна четверная доля – четвертью .
Для краткости записи были введены следующие обозначения долей . Одну вторую долю обозначают как или 1/2 , одну третью долю – как или 1/3 ; одну четвертую долю – как или 1/4 , и так далее. Отметим, что запись с горизонтальной чертой употребляется чаще. Для закрепления материала приведем еще один пример: запись обозначает одну сто шестьдесят седьмую долю целого.
Понятие доли естественным образом распространяется с предметов на величины. Например, одной из мер измерения длины является метр. Для измерения длин меньших, чем метр, можно использовать доли метра. Так можно воспользоваться, например, половиной метра или десятой или тысячной долей метра. Аналогично применяются доли других величин.
Обыкновенные дроби, определение и примеры дробей
Для описания количества долей используются обыкновенные дроби . Приведем пример, который позволит нам подойти к определению обыкновенных дробей.
Пусть апельсин состоит из 12 долей. Каждая доля в этом случае представляет одну двенадцатую долю целого апельсина, то есть, . Две доли обозначим как , три доли – как , и так далее, 12 долей обозначим как . Каждую из приведенных записей называют обыкновенной дробью.
Теперь дадим общее определение обыкновенных дробей .
Озвученное определение обыкновенных дробей позволяет привести примеры обыкновенных дробей
: 5/10
, , 21/1
, 9/4
, . А вот записи  не подходят под озвученное определение обыкновенных дробей, то есть, не являются обыкновенными дробями.
не подходят под озвученное определение обыкновенных дробей, то есть, не являются обыкновенными дробями.
Числитель и знаменатель
Для удобства в обыкновенной дроби различают числитель и знаменатель .
Определение.
Числитель обыкновенной дроби (m/n ) – это натуральное число m .
Определение.
Знаменатель обыкновенной дроби (m/n ) – это натуральное число n .
Итак, числитель расположен сверху над чертой дроби (слева от наклонной черты), а знаменатель – снизу под чертой дроби (справа от наклонной черты). Для примера приведем обыкновенную дробь 17/29 , числителем этой дроби является число 17 , а знаменателем – число 29 .
Осталось обговорить смысл, заключенный в числителе и знаменателе обыкновенной дроби. Знаменатель дроби показывает, из скольких долей состоит один предмет, числитель в свою очередь указывает количество таких долей. Например, знаменатель 5 дроби 12/5 означает, что один предмет состоит из пяти долей, а числитель 12 означает, что взято 12 таких долей.
Натуральное число как дробь со знаменателем 1
Знаменатель обыкновенной дроби может быть равен единице. В этом случае можно считать, что предмет неделим, иными словами, представляет собой нечто целое. Числитель такой дроби указывает, сколько целых предметов взято. Таким образом, обыкновенная дробь вида m/1 имеет смысл натурального числа m . Так мы обосновали справедливость равенства m/1=m .
Перепишем последнее равенство так: m=m/1 . Это равенство дает нам возможность любое натуральное число m представлять в виде обыкновенной дроби. Например, число 4 – это дробь 4/1 , а число 103 498 равно дроби 103 498/1 .
Итак, любое натуральное число m можно представить в виде обыкновенной дроби со знаменателем 1 как m/1 , а любую обыкновенную дробь вида m/1 можно заменить натуральным числом m .
Черта дроби как знак деления
Представление исходного предмета в виде n долей представляет собой не что иное как деление на n равных частей. После того как предмет разделен на n долей, мы его можем разделить поровну между n людьми – каждый получит по одной доле.
Если же у нас есть изначально m одинаковых предметов, каждый из которых разделен на n долей, то эти m предметов мы можем поровну разделить между n людьми, раздав каждому человеку по одной доле от каждого из m предметов. При этом у каждого человека будет m долей 1/n , а m долей 1/n дает обыкновенную дробь m/n . Таким образом, обыкновенную дробь m/n можно применять для обозначения деления m предметов между n людьми.
Так мы получили явную связь между обыкновенными дробями и делением (смотрите общее представление о делении натуральных чисел). Эта связь выражается в следующем: черту дроби можно понимать как знак деления, то есть, m/n=m:n .
С помощью обыкновенной дроби можно записать результат деления двух натуральных чисел, для которых не выполняется деление нацело. Например, результат деления 5 яблок на 8 человек можно записать как 5/8 , то есть, каждому достанется пять восьмых долей яблока: 5:8=5/8 .
Равные и неравные обыкновенные дроби, сравнение дробей
Достаточно естественным действием является сравнение обыкновенных дробей , ведь понятно, что 1/12 апельсина отличается от 5/12 , а 1/6 доля яблока такая же, как другая 1/6 доля этого яблока.
В результате сравнения двух обыкновенных дробей получается один из результатов: дроби либо равны, либо не равны. В первом случае мы имеем равные обыкновенные дроби , а во втором – неравные обыкновенные дроби . Дадим определение равных и неравных обыкновенных дробей.
Определение.
равны , если справедливо равенство a·d=b·c .
Определение.
Две обыкновенные дроби a/b и c/d не равны , если равенство a·d=b·c не выполняется.
Приведем несколько примеров равных дробей. Например, обыкновенная дробь 1/2 равна дроби 2/4 , так как 1·4=2·2 (при необходимости смотрите правила и примеры умножения натуральных чисел). Для наглядности можно представить два одинаковых яблока, первое разрезано пополам, а второе – на 4 доли. При этом очевидно, что две четвертых доли яблока составляют 1/2 долю. Другими примерами равных обыкновенных дробей являются дроби 4/7 и 36/63 , а также пара дробей 81/50 и 1 620/1 000 .
А обыкновенные дроби 4/13 и 5/14 не равны, так как 4·14=56 , а 13·5=65 , то есть, 4·14≠13·5 . Другим примером неравных обыкновенных дробей являются дроби 17/7 и 6/4 .
Если при сравнении двух обыкновенных дробей выяснилось, что они не равны, то возможно потребуется узнать, какая из этих обыкновенных дробей меньше другой, а какая – больше . Чтобы это выяснить, используется правило сравнения обыкновенных дробей, суть которого сводится к приведению сравниваемых дробей к общему знаменателю и последующему сравнению числителей. Детальная информация по этой теме собрана в статье сравнение дробей: правила, примеры, решения .
Дробные числа
Каждая дробь является записью дробного числа . То есть, дробь – это всего лишь «оболочка» дробного числа, его внешний вид, а вся смысловая нагрузка содержится именно в дробном числе. Однако для краткости и удобства понятие дроби и дробного числа объединяют и говорят просто дробь. Здесь уместно перефразировать известное изречение: мы говорим дробь – подразумеваем дробное число, мы говорим дробное число – подразумеваем дробь.
Дроби на координатном луче
Все дробные числа, отвечающие обыкновенным дробям, имеют свое уникальное место на , то есть, существует взаимно однозначное соответствие между дробями и точками координатного луча.
Чтобы на координатном луче попасть в точку, соответствующую дроби m/n нужно от начала координат в положительном направлении отложить m отрезков, длина которых составляет 1/n долю единичного отрезка. Такие отрезки можно получить, разделив единичный отрезок на n равных частей, что всегда можно сделать с помощью циркуля и линейки.
Для примера покажем точку М на координатном луче, соответствующую дроби 14/10 . Длина отрезка с концами в точке O и ближайшей к ней точке, отмеченной маленьким штрихом, составляет 1/10 долю единичного отрезка. Точка с координатой 14/10 удалена от начала координат на расстояние 14 таких отрезков.

Равным дробям отвечает одно и то же дробное число, то есть, равные дроби являются координатами одной и той же точки на координатном луче. Например, координатам 1/2 , 2/4 , 16/32 , 55/110 на координатном луче соответствует одна точка, так как все записанные дроби равны (она расположена на расстоянии половины единичного отрезка, отложенного от начала отсчета в положительном направлении).
На горизонтальном и направленном вправо координатном луче точка, координатой которой является большая дробь, располагается правее точки, координатой которой является меньшая дробь. Аналогично, точка с меньшей координатой лежит левее точки с большей координатой.
Правильные и неправильные дроби, определения, примеры
Среди обыкновенных дробей различают правильные и неправильные дроби . Это разделение в своей основе имеет сравнение числителя и знаменателя.
Дадим определение правильных и неправильных обыкновенных дробей.
Определение.
Правильная дробь
– это обыкновенная дробь, числитель которой меньше знаменателя, то есть, если m Определение.
Неправильная дробь
– это обыкновенная дробь, в которой числитель больше или равен знаменателю, то есть, если m≥n
, то обыкновенная дробь является неправильной.
Приведем несколько примеров правильных дробей: 1/4
, , 32 765/909 003
. Действительно, в каждой из записанных обыкновенных дробей числитель меньше знаменателя (при необходимости смотрите статью сравнение натуральных чисел), поэтому они правильные по определению. А вот примеры неправильных дробей: 9/9
, 23/4
, . Действительно, числитель первой из записанных обыкновенных дробей равен знаменателю, а в остальных дробях числитель больше знаменателя. Также имеют место определения правильных и неправильных дробей, базирующиеся на сравнении дробей с единицей. Определение.
правильной
, если она меньше единицы.
Определение.
Обыкновенная дробь называется неправильной
, если она либо равна единице, либо больше 1
.
Так обыкновенная дробь 7/11
– правильная, так как 7/11<1
, а обыкновенные дроби 14/3
и 27/27
– неправильные, так как 14/3>1
, а 27/27=1
. Давайте поразмыслим, чем же обыкновенные дроби с числителем, превосходящим или равным знаменателю, заслужили такое название – «неправильные». Для примера возьмем неправильную дробь 9/9
. Эта дробь означает, что взято девять долей предмета, который состоит из девяти долей. То есть, из имеющихся девяти долей мы можем составить целый предмет. То есть, неправильная дробь 9/9
по сути дает целый предмет, то есть, 9/9=1
. Вообще, неправильные дроби с числителем равным знаменателю обозначают один целый предмет, и такую дробь может заменить натуральное число 1
. Теперь рассмотрим неправильные дроби 7/3
и 12/4
. Достаточно очевидно, что из этих семи третьих долей мы можем составить два целых предмета (один целый предмет составляют 3
доли, тогда для составления двух целых предметов нам потребуется 3+3=6
долей) и еще останется одна третья доля. То есть, неправильная дробь 7/3
по сути означает 2
предмета да еще 1/3
долю такого предмета. А из двенадцати четвертых долей мы можем составить три целых предмета (три предмета по четыре доли в каждом). То есть, дробь 12/4
по сути означает 3
целых предмета. Рассмотренные примеры приводят нас к следующему выводу: неправильные дроби, могут быть заменены либо натуральными числами, когда числитель делится нацело на знаменатель (например, 9/9=1
и 12/4=3
), либо суммой натурального числа и правильной дроби, когда числитель не делится нацело на знаменатель (например, 7/3=2+1/3
). Возможно, именно этим и заслужили неправильные дроби такое название – «неправильные». Отдельный интерес вызывает представление неправильной дроби в виде суммы натурального числа и правильной дроби (7/3=2+1/3
). Этот процесс называется выделением целой части из неправильной дроби , и заслуживает отдельного и более внимательного рассмотрения. Также стоит заметить, что существует очень тесная связь между неправильными дробями и смешанными числами . Каждая обыкновенная дробь отвечает положительному дробному числу (смотрите статью положительные и отрицательные числа). То есть, обыкновенные дроби являются положительными дробями
. К примеру, обыкновенные дроби 1/5
, 56/18
, 35/144
– положительные дроби. Когда нужно особо выделить положительность дроби, то перед ней ставится знак плюс, например, +3/4
, +72/34
. Если перед обыкновенной дробью поставить знак минус, то эта запись будет соответствовать отрицательному дробному числу. В этом случае можно говорить об отрицательных дробях
. Приведем несколько примеров отрицательных дробей: −6/10
, −65/13
, −1/18
. Положительная и отрицательная дроби m/n
и −m/n
являются противоположными числами . К примеру, дроби 5/7
и −5/7
– противоположные дроби. Положительные дроби, как и положительные числа в целом, обозначают прибавление, доход, изменение какой-либо величины в сторону увеличения и т.п. Отрицательные дроби отвечают расходу, долгу, изменению какой-либо величины в сторону уменьшения. Например, отрицательную дробь −3/4
можно трактовать как долг, величина которого равна 3/4
. На горизонтальной и направленной вправо отрицательные дроби располагаются левее начала отсчета. Точки координатной прямой, координатами которых являются положительная дробь m/n
и отрицательная дробь −m/n
расположены на одинаковом расстоянии от начала координат, но по разные стороны от точки O
. Здесь же стоит сказать о дробях вида 0/n
. Эти дроби равны числу нуль, то есть, 0/n=0
. Положительные дроби, отрицательные дроби, а также дроби 0/n
объединяются в рациональные числа . Одно действие с обыкновенными дробями – сравнение дробей - мы уже рассмотрели выше. Определены еще четыре арифметических действия с дробями
– сложение, вычитание, умножение и деление дробей. Остановимся на каждом из них. Общая суть действий с дробями аналогична сути соответствующих действий с натуральными числами. Проведем аналогию. Умножение дробей
можно рассматривать как действие, при котором находится дробь от дроби. Для пояснения приведем пример. Пусть у нас есть 1/6
часть яблока и нам нужно взять 2/3
части от нее. Нужная нам часть является результатом умножения дробей 1/6
и 2/3
. Результатом умножения двух обыкновенных дробей является обыкновенная дробь (которая в частном случае равна натуральному числу). Дальше рекомендуем к изучению информацию статьи умножение дробей – правила, примеры и решения . Список литературы.
Расширение дроби. Сокращение дроби. Сравнение дробей. Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется сокращением дроби. Например, Использованное здесь преобразование называется приведением дробей к общему знаменателю. Великий русский критик В. Г. Белинский сказал, что задача поэзии состоит в том, “чтобы извлекать поэзию жизни Из прозы жизни и потрясать души верным изображением жизни”. Именно таким писателем, писателем, потрясающим души изображением порой самых ничтожных картин существования человека в мире, является Н. В, Гоголь. Величайшая заслуга Гоголя перед русским обществом, на мой взгляд. Эта статья – попытка собрать воедино разнородную информацию относительно наиболее распространённого в среде любителей солнечных наблюдений телескопа. В той или иной степени она собрана на российских и зарубежных астрономических интернет-форумах, также в интернете собраны и все фотографии, размещённые ниже. Технические параметры, особенности конструкции, возможные. Десятичная система счисления Десятичная система счисления - позиционная система счисления по основанию 10. Наиболее распространённая система счисления в мире. Для записи чисел наиболее часто используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека. . Математика. 1 — 4 класс В этом разделе Вы познакомитесь с такими понятиями и терминами, как сложение, вычитание, умножение и деление. Так же вы познакомитесь с математическими действиями и порядком их выполнения, математическими сказками и многим – многим другим. . for-schoolboy.ru Сложение обыкновенных дробей выполняется так: а) если знаменатели дробей одинаковы, то к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель, т. е. б) если знаменатели дробей различны, то дроби сначала приводят к общему знаменателю, предпочтительнее к наименьшему, а затем применяют правило а). Пример 1. Сложить дроби и Решение. Имеем: Вычитание обыкновенных дробей выполняют следующим образом: а) если знаменатели дробей одинаковы, то б) если знаменатели различны, то сначала дроби приводят к общему знаменателю, а затем применяют правило а). Умножение обыкновенных дробей выполняют следующим образом: т. е. перемножают отдельно числители, отдельно знаменатели, первое произведение делают числителем, второе - знаменателем. Например, Деление обыкновенных дробей выполняют следующим образом: т. е. делимое умножают на дробь , обратную делителю Например, . Пример 2. Найти значение числового выражения Решение. 1) Сократив числитель и знаменатель на 3 (это полезно сделать до выполнения действий умножения в числителе и знаменателе), получим т. е. Итак 3) При нахождении значения выражения действия сложения и вычитания можно выполнять одновременно. Наименьшим общим кратным чисел 15, 20, 30 является число 60. Приведем все три дроби к знаменателю 60, использовав дополнительные множители: для первой дроби 4, для второй - 3, для третьей - 2. Получим: Пример 3. Выполнить действия: а) Решение, а) Первый способ. Обратим каждое из данных смешанных чисел в неправильную дробь, а затем выполним сложение: Обратим теперь неправильную дробь в смешанное число: Второй способ. Имеем б) В случае умножения и деления смешанных чисел всегда переходят к неправильным дробям: Значит, в 7 Разделы:
Математика 1) контроль и систематизация знаний учащихся по теме; 2) развивать вычислительные навыки, логику, математическую зоркость; 3) воспитывать самостоятельность, интерес к предмету, добросовестное отношение к учебному труду. ОБОРУДОВАНИЕ:
компьютерный класс, ПК- 9 шт 1) личностно-ориентированное обучение; 2) уровневая дифференциация; 3) игровая технология; 2. ПОСТАНОВКА ЦЕЛИ УРОКА. Сегодня на кануне контрольной работы у нас будет возможность проанализировать свою учебную деятельность и отработать вычислительные навыки выполнения всех действий с обыкновенными дробями на электронном тренажере. Уч-ся записывают на специально подготовленных листах число и наименование работы. 3. АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ Чтобы получить допуск к индивидуальной работе вы должны устно ответить на вопросы (у каждого на столе дидактический материал А.П Ершова, В.В.Голобородько «Устная математика»):
1. Сформулируйте основное свойство дроби. 2. Правило нахождения наименьшего общего знаменателя двух дробей. 3. Выполните сложение 4. Какие числа называются взаимно обратными? 5. Как разделить дробь на дробь? Уч-ся фронтально повторяют правила выполнения действий с обыкновенными дробями и выполняют задание с комментированием. 4. ИНСТРУКЦИЯ по выполнению этапов урока Сегодня у вас есть возможность проверить себя в 3-х номинациях: информатиков, математиков и аналитиков. Учащиеся делятся на 3 группы, и получают карты самоанализа (Приложение 1), соответственно которым проходят все этапы. (Учитель фиксирует оценки всех трех этапов и выставляет среднеарифметическое в картах команд Приложение 2)
На компьютере, на зачетных листах, по коррекционным карточкам или творческим заданиям 5. 1 этап
ЭЛЕКТРОННЫЙ ТРЕНАЖЕР (Приложении 3) — информатики Прежде всего ваш успех на этом этапе зависит от того на сколько внимательно вы будете выполнять правила игры « Биатлон» Тренировка состоит из трех этапов, отличающихся друг от друга сложностью заданий. Каждый этап включает «лыжную гонку» и «огневой рубеж». В режиме «лыжной гонки» требуется определить верным или неверным является предложенное утверждение и кликнуть мышью по соответствующей кнопке на экране. В режиме «на огневом рубеже» необходимо выполнить четыре (1 этап) или три (2 и 3 этапы) задания на вычисление суммы, разности, произведения или частного двух дробей. Ваш ответ — это выстрел по мишени. Вы попадаете в «яблочко», если Ваш ответ — несократимая дробь. Учитель фиксирует оценки выставленные компьютером. В карте команды.
Устная самостоятельная работа уч-ся.
Уч-ся устно отвечают на вопросы, выполняют действия и записывают результат на компьютере. А в карте самоанализа фиксируют свои ошибки. (каждый ученик группы за компьютером)
По окончанию игры компьютер оценивает ученика. 6. 2 этап
ЗАЧЕТ ПО ТЕОРИИ (А.П Ершова «Устная математика»):
— аналитики xn--i1abbnckbmcl9fb.xn--p1ai Подписано в печать с готовых диапозитивов 12.02.01. Формат 84х108/32. Гарнитура Балтика. Бумага тип. № 2. Печать офсетная. Усл. печ. л. 25,1. Тираж 5000 экз. Заказ № 106. Налоговая льгота - общероссийский классификатор продукции ОК-005-093, том 2; 953000- книги, брошюры. Отпечатано с готовых диапозитивов на ГИПП «Уральский рабочий», 620219, г. Екатеринбург, ул. Тургенева, 13. Тема №1.
Арифметические вычисления. Проценты.
Обыкновенные дроби. Действия над обыкновенными дробями.
1º. Натуральные числа
– это числа, употребляемые при счете. Множество всех натуральных чисел обозначают N, т.е. N= . Дробью
называется число, состоящее из нескольких долей единицы. Обыкновенной дробью
называется число вида , где натуральное число n
показывает, на сколько равных частей разделена единица, а натуральное число m
показывает, сколько таких равных частей взято. Числа m
и n
называют соответственно числителем
и знаменателем
дроби. Если числитель меньше знаменателя, то обыкновенная дробь называется правильной
; если числитель равен знаменателю или больше него, то дробь называется неправильной
. Число, состоящее из целой и дробной частей, называется смешанным числом
. Например, — правильные обыкновенные дроби, — неправильные обыкновенные дроби, 1 — смешанное число. 2º. При выполнении действий над обыкновенными дробями следует помнить следующие правила: 1) Основное свойство дроби
. Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной. Например, а) ; б) . Деление числителя и знаменателя дроби на их общий делитель, отличный от единицы, называется сокращением дроби
. 2) Чтобы смешанное число представить в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к полученному произведению прибавить числитель дробной части, записать полученную сумму числителем дроби, а знаменатель оставить прежним. Аналогично любое натуральное число можно записать в виде неправильной дроби с любым знаменателем. Например, а) , так как ; б) и т.д. 3) Чтобы неправильную дробь записать в виде смешанного числа (т.е. из неправильной дроби выделить целую часть), нужно числитель разделить на знаменатель, частное от деления взять в качестве целой части, остаток — в качестве числителя, знаменатель оставить прежним. Например, а) , так как 200: 7 = 28 (ост. 4); 4) Чтобы привести дроби к наименьшему общему знаменателю, надо найти наименьшее общее кратное (НОК) знаменателей этих дробей (оно и будет их наименьшим общим знаменателем), разделить наименьший общий знаменатель на знаменатели данных дробей (т.е. найти дополнительные множители для дробей), умножить числитель и знаменатель каждой дроби на ее дополнительный множитель. Например, приведем дроби к наименьшему общему знаменателю: 630: 18 = 35, 630: 10 = 63, 630: 21 = 30. Значит, ; ; . 5) Правила арифметических действий над обыкновенными дробями
: a) Сложение и вычитание дробей с одинаковыми знаменателями выполняется по правилу: b) Сложение и вычитание дробей с разными знаменателями выполняется по правилу a), предварительно приведя дроби к наименьшему общему знаменателю. c) При сложении и вычитании смешанных чисел можно обратить их в неправильные дроби, а затем выполнить действия по правилам a) и b), d) При умножении дробей пользуются правилом: e) Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю: f) При умножении и делении смешанных чисел, их предварительно переводят в неправильные дроби, а затем пользуются правилами d) и e). 1 Презентация к уроку «Действия с обыкновенными дробями» Выполнила учитель математики Колбина Евгения Викторовна 2 Цели урока. Обучающие: повторение правил сравнения, сложения, вычитания, умножения и деления обыкновенных дробей; обобщение и систематизация знаний об обыкновенных дробях, закрепление и усовершенствование навыков действий с обыкновенными дробями; отработка навыков устного счета и умения применять правила при решении более сложных примеров. Развивающие: развитие умений учебно-познавательной деятельности; развитие культуры устной и письменной речи; развитие навыков самоконтроля и самооценки достигнутых знаний и умений. Воспитательные: воспитание внимательности, активности, самостоятельности, ответственности. 3 Без чего не могут обойтись математики, барабанщики и даже охотники? 4 Какой сейчас месяц? Какое время года? Чем вам нравится зима? 5 Сегодня на уроке мы с вами будем лепить снеговика, только не из снега, а из наших знаний 6 Оценочный лист (Ф.И. ученика) « Сугробы »« 1 ком »« 2 ком »« 3 ком »« Атрибуты » Итого Оценка 7 1. Чтобы сравнить (сложить, вычесть) дроби с разными, надо: 1) привести данные дроби к; 2) сравнить (сложить, вычесть) полученные дроби. 2. Чтобы сложить (вычесть) смешанные числа, надо: 1) привести дробные части к; 2) отдельно выполнить сложение (вычитание) частей и дробных частей. 3. Чтобы умножить дробь на натуральное число, надо ее умножить на это число, а оставить без изменения. знаменателямиНОЗ (наименьшему общему знаменателю) НОЗ целых числитель знаменатель 4. Чтобы умножить дробь на дробь, надо найти произведение и произведение. 5. Для того, чтобы выполнить умножение смешанных чисел, надо их записать в виде дробей, а затем воспользоваться правилом дробей. 6. Чтобы разделить одну дробь на другую, нужно умножить на число, делителю. числителейзнаменателей неправильных умножения делимое обратное «СУГРОБЫ» За каждое верное правило – 1 балл 8 «1 ком» За каждый верный ответ – 1 балл 10 I Вариант 635(а) II Вариант 635(б) «2 ком» За каждое верное действие – 1 балл 12 Трава маленькая-маленькая. Деревья высокие-высокие. Ветер деревья качает-качает. То направо, то налево наклоняет. То вверх, то назад. То вниз сгибает. Птицы летят-улетают. Ученики тихонько за парты садятся. Физминутка 13 Задача Туристы отправились в поход. В первый день они прошли км, что на км больше, чем во второй день. А в третий день они прошли в 2 раза меньше, чем в первый. Сколько километров туристы прошли за эти три дня? «3 ком» 14 1) найдем, сколько туристы прошли во второй день, для этого из отнимем 2) найдем, сколько туристы прошли в третий день, для этого разделим на 2 3) сложим, результат 1 действия и результат второго действия и найдем, сколько они прошли за эти три дня. Ответ: План решения За каждое верное действие – 1 балл + 1 балл за верный ответ 16 Тест «Атрибуты» За каждый верный ответ 1 балл 18 27-30 баллов – «5» баллов – «4» баллов – «3» 0-14 баллов – «2» 19 Домашнее задание: 635 (г), 643 Приготовить доклад на тему: происхождение обыкновенных дробей 20 Итог урока Все понравилось! Сложно, но интересно! Устал! 21 Великий русский писатель Л.Н. Толстой считал, что человек похож на дробь, знаменатель которой — это то, что он думает о себе, а числитель- это то, что думают о нем. Я желаю вам, чтобы числитель в вашей жизни был больше знаменателя.Положительные и отрицательные дроби
Действия с дробями
Приведение к общему знаменателю. Сложение и вычитание дробей.
Умножение дробей. Деление дробей.
Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется расширением дроби. Например, 
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:
Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше: 
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.
П р и м е р. Сравнить две дроби:
Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.
П р и м е р. 
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.
П р и м е р. 
Деление дробей. Для того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь. Это правило вытекает из определения деления (см. раздел “Арифметические операции”).
П р и м е р. 
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Действия с обыкновенными дробями
Обыкновенные дроби. Действия над обыкновенными дробями
б) , так как 20: 5 = 4 (ост. 0).Презентация по предмету «Математика» на тему: «Презентация к уроку «Действия с обыкновенными дробями» Выполнила учитель математики Колбина Евгения Викторовна.». Скачать бесплатно и без регистрации. - Транскрипт: